¿Qué son los árboles de decisión?

En pocas palabras, un árbol de decisión es un árbol en el que cada nodo de rama representa una elección entre varias alternativas y cada nodo de hoja representa una decisión.

Es un tipo de algoritmo de aprendizaje supervisado (con una variable de destino predefinida) que se utiliza principalmente en problemas de clasificación y funciona para variables de entrada y salida tanto categóricas como continuas. Es uno de los métodos más utilizados y prácticos para la inferencia inductiva. (La inferencia inductiva es el proceso de llegar a una conclusión general a partir de ejemplos específicos) y en la minería de datos.

Los árboles de decisión aprenden y se entrenan a partir de ejemplos dados y predicen para circunstancias no vistas.

Una representación gráfica de un árbol de decisión de muestra podría ser:

Algoritmo del Árbol de Decisiones: ID3

ID3 significa Iterative Dichotomizer 3. El algoritmo ID3 fue inventado por Ross Quinlan. Construye un árbol de decisiones a partir de un conjunto fijo de ejemplos y el árbol resultante se usa para clasificar muestras futuras.

La idea básica es construir el árbol de decisiones empleando una búsqueda codiciosa de arriba hacia abajo a través de los conjuntos dados para probar cada atributo en cada nodo de árbol.

Suena simple, pero ¿qué nodo deberíamos seleccionar para construir el árbol de decisión correcto y más preciso? ¿Cómo decidiríamos eso?

Bueno, tenemos algunas medidas que pueden ayudarnos a seleccionar la mejor opción.

Entropía

En teoría de la información, la entropía es una medida de la incertidumbre sobre una fuente de mensajes. Nos da el grado de desorganización en nuestros datos.

Dada una colección S que contiene ejemplos positivos y negativos de algún concepto objetivo, la entropía de S relativa a esta clasificación booleana es:

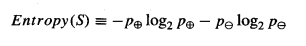
Aquí, p + y p- son la proporción de ejemplos positivos y negativos en S.

Considere esta función de entropía relativa a una clasificación booleana, ya que la proporción de ejemplos positivos p + varía entre 0 y 1.

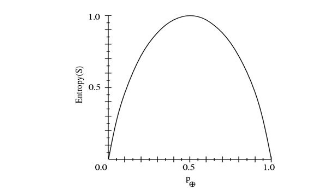
Observe que la entropía es 0 si todos los miembros de S pertenecen a la misma clase. Por ejemplo, si todos los miembros son positivos (p + = 1), entonces p- es 0 y Entropy (S) = -1. log2 (1) - 0. log2 0 = -1. 0 - 0. log2 0 = 0.

La entropía es 1 cuando la colección contiene una cantidad igual de ejemplos positivos y negativos.

Si la colección contiene números desiguales de ejemplos positivos y negativos, la entropía está entre 0 y 1.

Ganancia de información

Mide la reducción esperada en entropía. Decide qué atributo va a un nodo de decisión. Para minimizar la profundidad del árbol de decisión, ¡el atributo con la mayor reducción de entropía es la mejor opción!

Más precisamente, la Ganancia (Gain) de ganancia de información (S, A) de un atributo A con respecto a una colección de ejemplos S se define como:

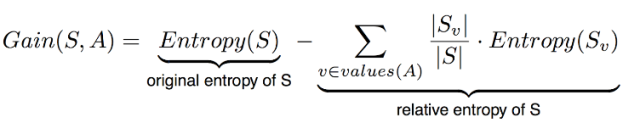
S = Cada valor v de todos los valores posibles del atributo A

Sv = Subconjunto de S para el cual el atributo A tiene valor v

| Sv | = Número de elementos en Sv

| S | = Número de elementos en S

Supongamos que queremos que ID3 decida si el clima es bueno para jugar al béisbol. En el transcurso de dos semanas, se recopilan datos para ayudar a ID3 a construir un árbol de decisiones. La clasificación objetivo es "¿deberíamos jugar al béisbol?", Que puede ser sí o no.

Los atributos climáticos son la vista, la temperatura, la humedad y la velocidad del viento. Pueden tener los siguientes valores:

vista = {soleado, nublado, lluvia}

temperatura = {caliente, suave, fresco}

humedad = {alto, normal}

viento = {débil, fuerte}

Necesitamos encontrar qué atributo será el nodo raíz en nuestro árbol de decisión.

Entropía (S) = - (9/14) Log2 (9/14) - (5/14) Log2 (5/14) = 0.940

Ganancia (S, Viento) = Entropía (S) - (8/14) * Entropía (Succión) - (6/14) * Entropía (Sstrong)

= 0.940 - (8/14) * 0.811 - (6/14) * 1.00

= 0.048

Entropía (Sdebil) = - (6/8) * log2 (6/8) - (2/8) * log2 (2/8) = 0.811

Entropía (Sfuerte) = - (3/6) * log2 (3/6) - (3/6) * log2 (3/6) = 1.00

Para cada atributo, la ganancia se calcula y la mayor ganancia se usa en la decisión.

Ganancia (S, Vista) = 0.246

Ganancia (S, temperatura) = 0.029

Ganancia (S, Humedad) = 0.151

Claramente, el atributo Vista tiene la mayor ganancia. Por lo tanto, se usa como el atributo de decisión en el nodo raíz.

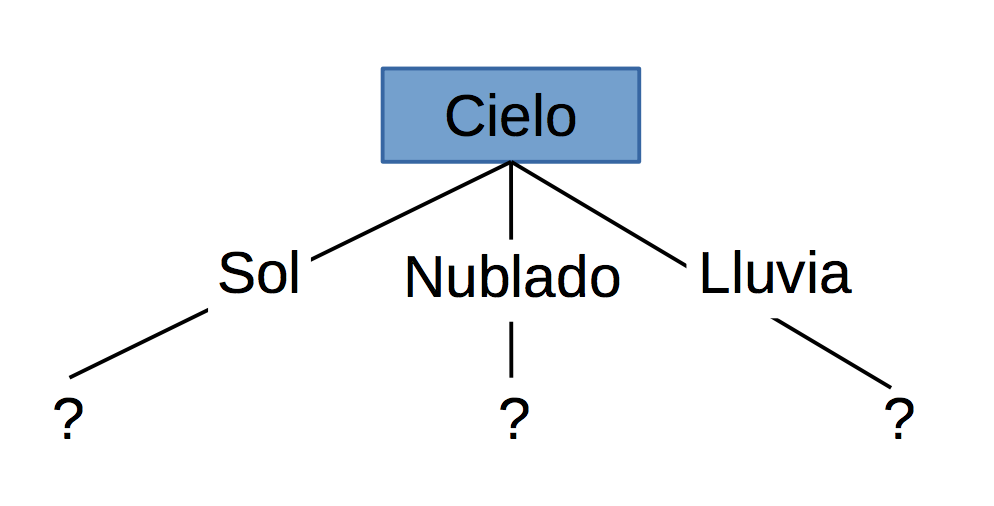
Como la perspectiva tiene tres valores posibles, el nodo raíz tiene tres ramas (soleado, nublado, lluvia). La siguiente pregunta es: ¿Qué atributo debería probarse en el nodo soleado de la rama? Como hemos utilizado Vista en la raíz, solo decidimos los tres atributos restantes: humedad, temperatura o viento.

Ssoleado = {D1, D2, D8, D9, D11} = 5 ejemplos de la tabla con vista = soleado

Ganancia (Ssoleado, Humedad) = 0.970

Ganancia (Ssoleado, temperatura) = 0.570

Ganancia (Ssoleado, Viento) = 0.019

La humedad tiene la mayor ganancia; por lo tanto, se usa como nodo de decisión. Este proceso continúa hasta que todos los datos se clasifiquen perfectamente o nos quedemos sin atributos.

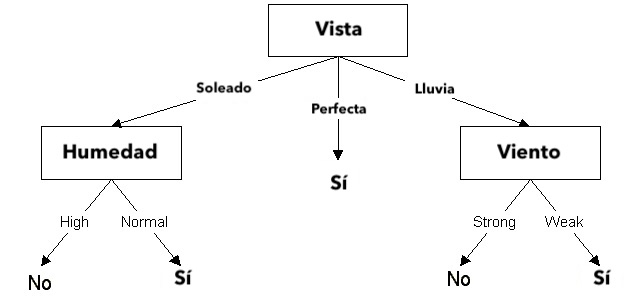
El árbol de decisión también se puede expresar en formato de regla:

IF vista = soleado AND humedad = alta THEN jugar beisbol = no

IF vista = lluvia AND humedad = alta THEN jugar beisbol = no

IF vista = lluvia AND viento = fuerte THEN jugar beisbol = yes

IF vista = perfecta THEN jugar beisbol = yes

IF vista = lluvia AND viento = débil THEN jugar beisbol = yes

Entonces, esa fue una introducción muy rápida a los árboles de decisión. Es tan simple como se muestra arriba.