La estadística es básicamente una ciencia que implica la recopilación de datos, la interpretación de datos y, finalmente, la validación de datos. El análisis de datos estadístico es un procedimiento para realizar diversas operaciones estadísticas.

Es un tipo de investigación cuantitativa que busca cuantificar los datos y, por lo general, aplica alguna forma de análisis estadístico.

Los datos cuantitativos básicamente involucran datos descriptivos, como datos de encuestas y datos de observación.

El análisis de datos estadísticos generalmente involucra alguna forma de herramientas estadísticas. Hay varios paquetes de software para realizar análisis de datos estadísticos.

Estos software incluyen el Sistema de análisis estadístico (SAS), el Paquete estadístico para las ciencias sociales (SPSS), Stat soft, R, etc.

Los datos en el análisis de datos estadísticos consisten en variables. En ocasiones, los datos son univariados o multivariantes. Dependiendo del número de variables, el investigador usa diferentes técnicas estadísticas.

Si los datos en el análisis de datos estadísticos son múltiples en números, entonces se pueden realizar varios multivariados. Estos son análisis de datos estadísticos factoriales, análisis de datos estadísticos discriminantes, etc.

De forma similar, si los datos son singulares en número, entonces se realiza el análisis de datos estadísticos univariado. Esto incluye la prueba t para significancia, prueba z, prueba f, ANOVA, etc.

Tipos de Datos en el análisis estadístico

- Tipos de Datos estadísticos

- Herramientas para realizar análisis estadístico

Los datos en el análisis de datos estadístico son básicamente de 2 tipos, datos continuos y datos discretos. La información continua es la que no puede ser contada. Por ejemplo, la intensidad de una luz puede medirse pero no puede contarse. La información discreta es la que puede ser contada. Por ejemplo, se puede contar el número de bombillas.

Los datos continuos en el análisis de datos estadísticos se distribuyen bajo la función de distribución continua, que también se puede llamar función de densidad de probabilidad o fdp.

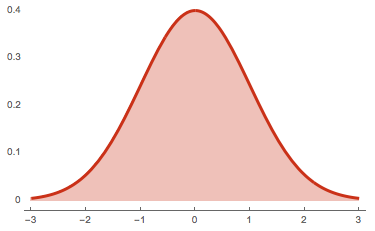
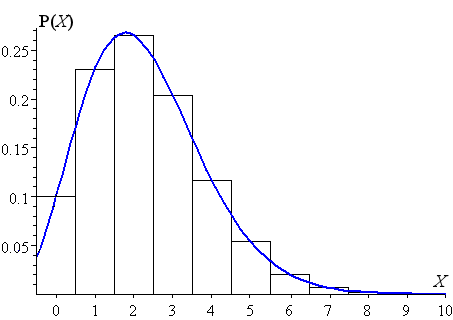
Los datos discretos en el análisis de datos estadísticos se distribuyen bajo la función de distribución discreta, que también se puede llamar la función de masa de probabilidado fmp.

Usamos la palabra "densidad" en datos continuos de análisis de datos estadísticos porque la densidad no se puede contar, pero se puede medir. Usamos la palabra "masa" en datos discretos de análisis de datos estadísticos porque la masa no se puede contar.

Hay varias fdp y fmp en el análisis de datos estadísticos. Por ejemplo, la distribución de Poisson es la fmp comúnmente conocida, y la distribución normal es la fdp comúnmente conocida.

Estas distribuciones en el análisis de datos estadísticos nos ayudan a comprender qué datos corresponden a qué distribución. Si los datos son sobre la intensidad de una bombilla, entonces los datos caerían en la distribución de Poisson.

Hay una tarea importante en el análisis de datos estadísticos, que se compone de inferencia estadística. La inferencia estadística se compone principalmente de dos partes: estimación y pruebas de hipótesis.

La estimación en el análisis de datos estadísticos implica principalmente datos paramétricos: los datos que constan de parámetros.

Por otro lado, las pruebas de hipótesis en el análisis de datos estadísticos implican principalmente datos no paramétricos, los datos que no constan de parámetros.

Sugerimos comenzar sus esfuerzos de análisis de datos con los siguientes cinco principios básicos y aprender a evitar sus problemas antes de avanzar hacia técnicas más sofisticadas.

Medidas Principales

Media

La media aritmética, más comúnmente conocida como "el promedio", es la suma de una lista de números dividida por el número de elementos en la lista.

La media es útil para determinar la tendencia general de un conjunto de datos o proporcionar una instantánea rápida de sus datos. Otra ventaja de la media es que es muy fácil y rápida de calcular.

Problemas

Tomado sola, la media es una herramienta peligrosa. En algunos conjuntos de datos, la media también está estrechamente relacionada con el modo y la mediana (otras dos medidas cercanas al promedio).

Sin embargo, en un conjunto de datos con un alto número de valores atípicos o una distribución sesgada, el promedio simplemente no proporciona la precisión que necesita para una decisión.

Desviación estándar

La desviación estándar, a menudo representada con la letra griega sigma, es la medida de una dispersión de datos alrededor de la media.

Una desviación estándar alta significa que los datos se distribuyen más ampliamente desde la media, donde una baja desviación estándar indica que más datos se alinean con la media.

Dentro de los métodos de análisis de datos, la desviación estándar es útil para determinar rápidamente la dispersión de puntos de datos.

Problemas

Al igual que la media, la desviación estándar es engañosa si se toma sola. Por ejemplo, si los datos tienen un patrón muy extraño, como una curva no normal o una gran cantidad de valores atípicos, la desviación estándar no le dará toda la información que necesita.

Regresión

La regresión modela las relaciones entre variables dependientes y explicativas, que generalmente se grafican en un diagrama de dispersión. La línea de regresión también designa si esas relaciones son fuertes o débiles.

La regresión se enseña comúnmente en cursos de estadística de la escuela secundaria o la universidad con aplicaciones para la ciencia o los negocios para determinar tendencias a lo largo del tiempo.

Problemas

La regresión no es muy matizada. A veces, los valores atípicos en un diagrama de dispersión (y las razones para ellos) son importantes.

Por ejemplo, un punto de datos periférico puede representar la entrada de su proveedor más crítico o su producto más vendido.

La naturaleza de una línea de regresión, sin embargo, lo tienta a ignorar estos valores atípicos. 

Tamaño de la muestra

Al medir un gran conjunto de datos o población, como una fuerza de trabajo, no siempre es necesario recopilar información de cada miembro de esa población: una muestra puede ser suficiente. El truco es determinar el tamaño correcto para que una muestra sea precisa.

Usando métodos de proporción y desviación estándar, puede determinar con precisión el tamaño de muestra correcto que necesita para hacer que su recopilación de datos sea estadísticamente significativa.

Problemas

Al estudiar una nueva variable no probada en una población, sus ecuaciones de proporción podrían necesitar ciertas suposiciones. Sin embargo, estas suposiciones pueden ser completamente inexactas. Este error luego se transfiere a la determinación del tamaño de la muestra y luego al resto de su análisis de datos estadísticos.

Pruebas de hipótesis

También comúnmente denominado prueba t, la prueba de hipótesis evalúa si una determinada premisa es realmente cierta para su conjunto de datos o población. En el análisis de datos y las estadísticas, considera que el resultado de una prueba de hipótesis es estadísticamente significativa si los resultados no pudieron haber ocurrido por casualidad.

Las pruebas de hipótesis se utilizan en todo, desde la ciencia y la investigación hasta los negocios y la economía.

Problemas

Para ser riguroso, las pruebas de hipótesis deben tener en cuenta los errores comunes. Por ejemplo, el efecto placebo ocurre cuando los participantes esperan falsamente un determinado resultado y luego perciben (o realmente alcanzan) ese resultado.

Otro error común es el efecto Hawthorne (o efecto observador), que ocurre cuando los participantes sesgan los resultados porque saben que están siendo estudiados.

Herramientas

Hay una gran cantidad de herramientas disponibles para llevar a cabo análisis estadísticos de datos, y a continuación te presentamos las mejores de ellas. 

SPSS (IBM)

Este es quizás el paquete de software de estadísticas más utilizado dentro de la investigación del comportamiento humano. SPSS ofrece la capacidad de compilar fácilmente estadísticas descriptivas, análisis paramétricos y no paramétricos, así como representaciones gráficas de resultados a través de la interfaz gráfica de usuario (GUI).

R

R es un paquete de software estadístico gratuito que se utiliza ampliamente tanto en la investigación del comportamiento humano como en otros campos. Las cajas de herramientas (esencialmente complementos) están disponibles para una gran variedad de aplicaciones, lo que puede simplificar varios aspectos del procesamiento de datos.

MATLAB

MatLab es una plataforma analítica y un lenguaje de programación ampliamente utilizado por ingenieros y científicos. Al igual que con R, el camino de aprendizaje es empinado y se te pedirá que creas tu propio código en algún momento.

Microsoft Excel

Si bien no es una solución de vanguardia para el análisis estadístico, MS Excel ofrece una amplia variedad de herramientas para la visualización de datos y estadísticas simples. Es sencillo generar métricas de resumen y gráficos y figuras personalizables, lo que lo convierte en una herramienta útil para muchos que desean ver los conceptos básicos de sus datos.

SAS

SAS es una plataforma de análisis estadístico que ofrece opciones para usar la GUI o crear scripts para análisis más avanzados. Es una solución Premium que se usa ampliamente en negocios, atención médica y en la investigación del comportamiento humano por igual.

Es posible realizar análisis avanzados y producir gráficos y cuadros dignos de publicación, aunque la codificación también puede ser un ajuste difícil para aquellos que no están acostumbrados a este enfoque.